2進数の論理演算
2進数(0,1)には,たし算やかけ算など普通の算術演算の他に,論理演算という重要な演算があります。
計算というよりは,0と1を用いた論理展開のようなもので,プログラム中でも頻繁に現れます。
はじめに論理演算の基本である論理和と論理積について次の例を示しましょう。
論理和
皆さんは数学の講義を受講しています。講義には中間試験と期末試験があり,試験の結果が60点以上であれば1,60点未満であれば0とします。
表1の左側に試験結果を0,1の4通りの組み合わせで示してあります。
| 入力(試験結果) | 出力(成績) | ||
|---|---|---|---|
| 60点以上:1 / 60点未満:0 | 合格:1 / 不合格:0 | ||
| 中間試験 | 期末試験 | どちらか一方が 60点以上であれば合格 | 両方とも 60点以上であれば合格 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
まず,表1.2.2の3列目に示すように,2つの試験のどちらか一方でも60点以上であれば合格としましょう。講義の合格を1,不合格を0で表すと,両試験とも0の場合のみ0(不合格)で,どちらかが1であれば1(合格)となります。この考え方が論理和(OR)です。「中間試験が60点以上 または(OR) 期末試験が60点以上であれば1(合格)」という考え方です。論理和の記号を「|」で表すと,論理和の演算は,
0|0=0,0|1=1,1|0=1,1|1=1
の4通りで表されます。1|1以外はたし算(算術和)と同じです。
論理積
次に,表1の4列目に示すように,2つの試験の両方とも60点以上であれば合格としましょう。両試験とも1の場合のみ1(合格)でそれ以外は0(不合格)になります。この考え方が論理積(AND)です。
「中間試験が60点以上 かつ(AND) 期末試験が60点以上であれば1(合格)」という考え方です。論理積の記号を「&」で表すと,論理積の演算は,
0&0=0,0&1=0,1&0=0,1&1=1
の4通りで表されます。
この4通りに限れば,かけ算(算術積)と同じになります。
否定
論理積・論理和の他にもう1つ重要な論理演算があります。それは,否定(NOT)あるいは反転とよばれるもので,0を1に,1を0にするものです。記号「~」で表すと,
~0=1,~1=0
となります。否定は次のように考えましょう。
試験に合格すれば当然再試験の必要はありませんが,不合格であれば再試験を受けなければならないとします。再試ありを1,再試なしを0とすると,表1.2.3のように合否と再試の関係は否定の関係,
(再試の有無)=~(試験の合否)
になります。
| 試験の合否(1/0) | 再試の有無(1/0) |
|---|---|
| 0 | 1 |
| 1 | 0 |
論理和,論理積,否定の回路記号
以上みてきたように,論理演算は,算数の計算というよりは,入力の組み合わせによる判断に用いられます。
プログラムの他,デジタル回路の中でデジタル信号の制御にも使われます。図1に論理和,論理積,否定の回路記号を示します
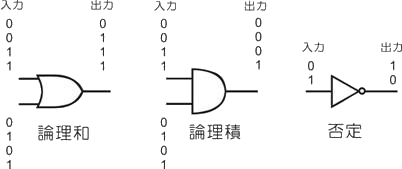
図1 論理和,論理積,否定の回路記号
なお,2進数のたし算(算術和)やかけ算(算術積)はとても簡単です。
※永田照三 戎俊男 太田信二郎 江藤昭弘 水野隆 石野健英 藤間信久 東直人 井上修次『作って学ぶ ロボット入門講座』より


