電気・電子の基礎とソフトウェア無線について学ぶ講義ビデオ付き組み立てキット

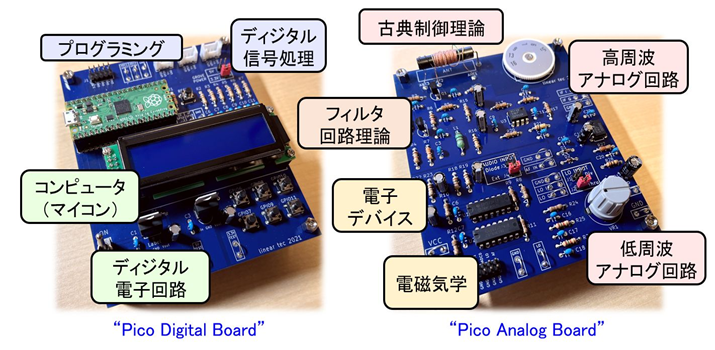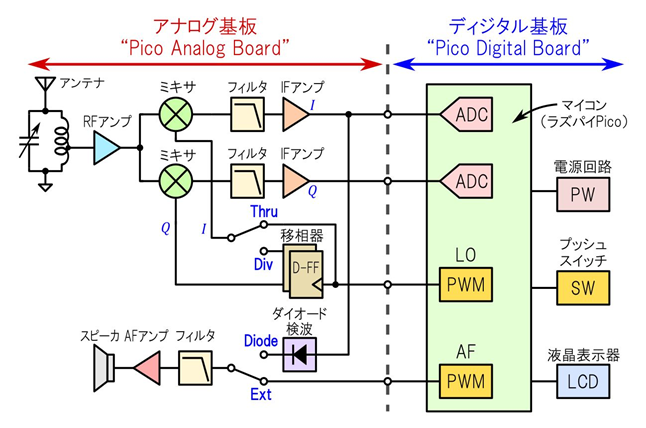
実習用組み立てキット“Pico Stack SDR”を構成するPico Digital BoardとPico Analog Board

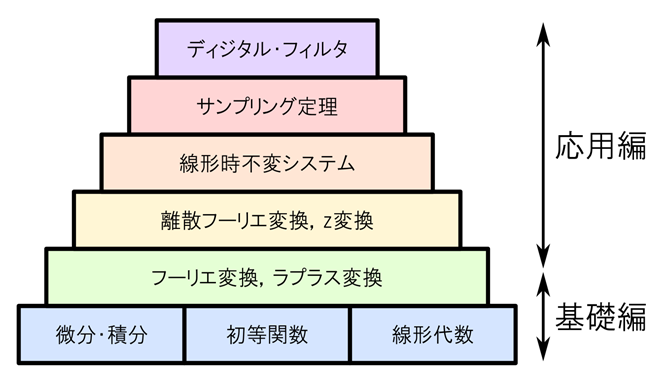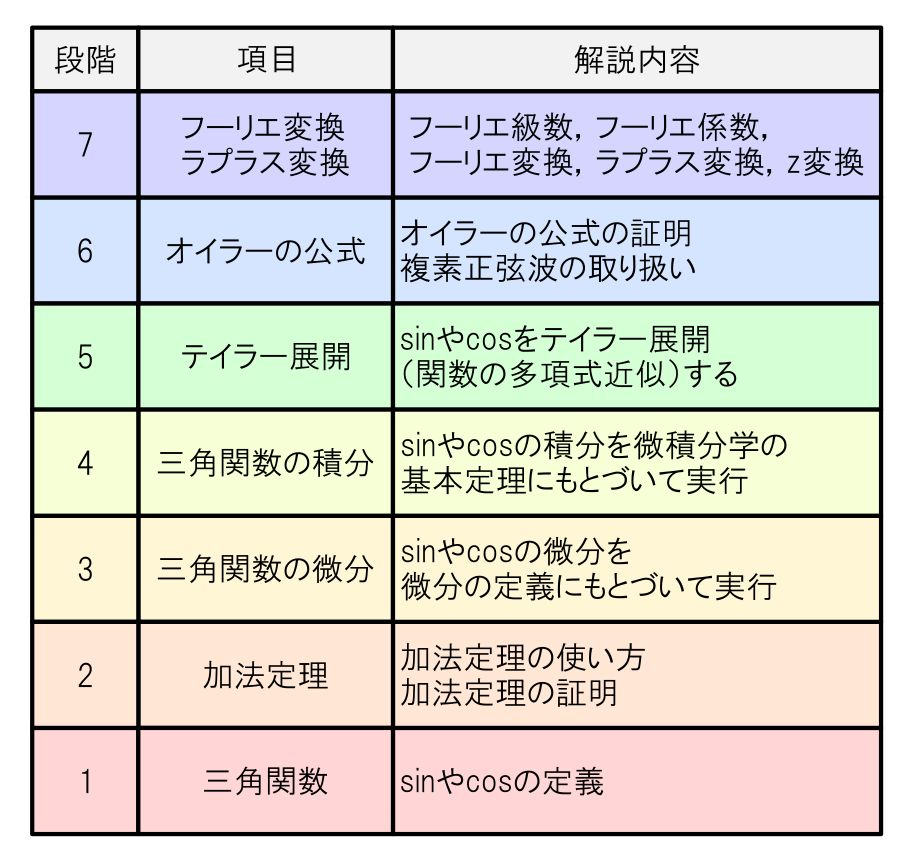「基礎編」と「応用編」の内容	本セミナで解説する理論の階層構造

■セット内容一覧

①講義資料一式

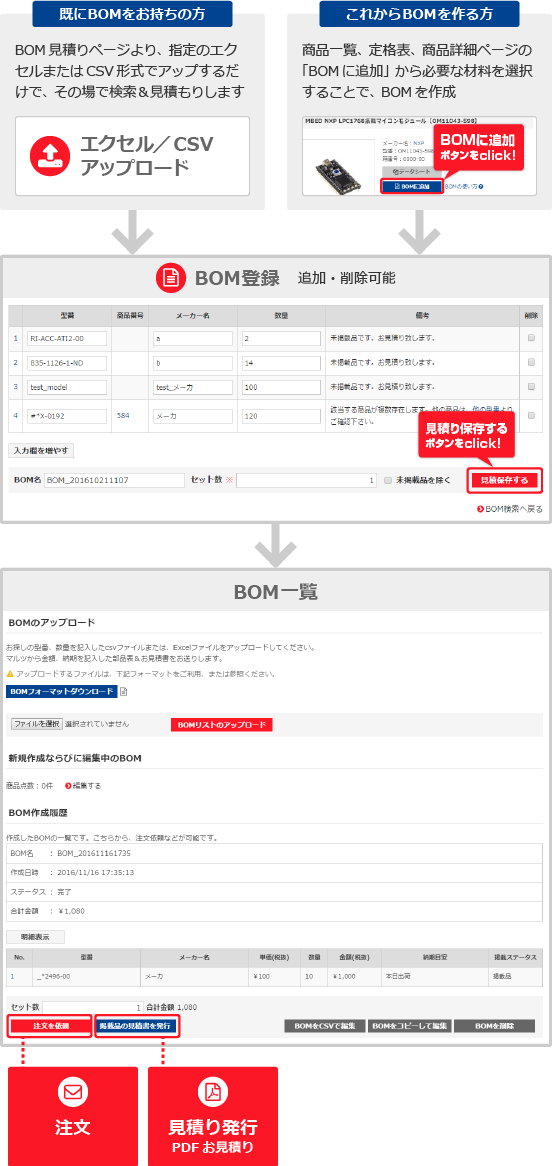
1．ソフトウェア・ラジオ 学習キット Pico Stack SDR“mz-picostacksdr”
2．全800分の講義ビデオ
　同梱の説明書にパスワードが記載されています
3．講義テキスト
　同梱の説明書にパスワードが記載されています

ソフトウェア無線の信号処理技術を学習できる組立キットの構成パーツ	完成状態(はんだ付けが必要です)

②実習用組立キットと技術資料一式

1. 1_PicoStackSDR_部品表_20220401.pdf
2. 2_PicoStackSDR_組み立てマニュアル_20220401.pdf
3. 3_PicoStackSDR_使い方マニュアル_20220401.pdf
4. 4_PicoStackSDR_回路図_20220401.pdf

■講義ビデオの内容

●基礎編

「ディジタル信号処理」に必要な数学を高校数学から始めて一気通貫で解説します．「初等関数」（三角関数，指数関数，対数関数），「微分・積分」，「複素平面」，「オイラーの公式」，「フーリエ解析の基礎」などを扱います．これらの基本的な内容を徹底的に理解すれば，ディジタル信号処理にとどまらず回路設計や制御工学，統計解析，その他のあらゆるエンジニアリング手法を身に着ける際に大いに役立ちます．

・電子工学の集大成である“SDR”（ソフトウェア無線機）を題材にして，「エンジニアにはどんな理論が必要なの？」という疑問に答えます！・「設計」に必須のテクニックである「微分」と「積分」の意味や使い方を演習形式で徹底的に解説します！

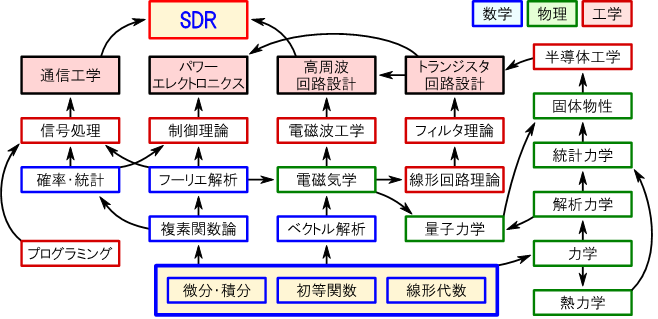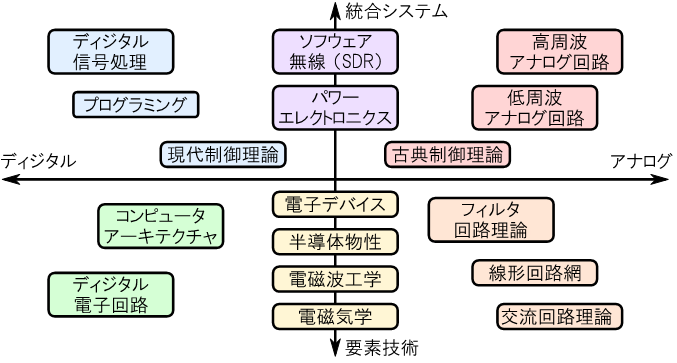理論の地図	電気・電子工学の全体像

●応用編

「基礎編」で扱った各種初等関数，微分・積分，複素平面，オイラーの公式などの理解を前提として，実際のディジタル信号処理システムの設計に必要な「フーリエ変換」，「離散フーリエ変換」，「$z$変換」，「サンプリング定理」，「ディジタル・フィルタ設計」を解説します．最終的にSDRキット“Pico Stack SDR”で実際に使用している信号処理のソース・コードを理解することを目指します．

・電気回路，機械設計，情報工学，あらゆるエンジニアリングには「フーリエ解析」が必須です！
・本セミナ（応用編）では，「フーリエ解析」の本質を最高にわかりやすく解説します！
・フーリエ解析の応用として「微分方程式を解く」，「ディジタル・フィルタを設計する」などの具体例も扱います！

“Pico Stack SDR”のシステム・ブロック図	「フィルタ設計」と「微分・積分」のかかわり

■本製品を購入された方へ「講義ビデオと講義テキストのリンク先」

下記リンク先(青字)をクリックし，本製品同梱の説明書に書かれたパスワードを入力してください．

講義ビデオ(著作権保護のためパスワードがかけられています)

●20220226_初めてのソフトウェア無線セミナ【基礎編】_Part1.mp4(2時間37分08秒)

・0:00:00 イントロダクション
目標はエンジニアリングのすべての分野に共通する「微分・積分 と 設計 の結びつき」を理解すること．複素正弦波 $e^{j\omega t}$はあらゆる分野で使うので押さえたい．$e^{j\omega t}$ の微分・積分から「フィルタの原理」へ．
・0:07:40 Pico Stack SDR の紹介
通信機，とくに ソフトウェア無線機 を作れば全部学べる．電気・電子工学はとにかく「アンプ」と「フィルタ」が主役．そしてSDRは電気電子工学の集大成である．「ラズパイPico」の能力を出し切った Pico Stack SDRを紹介．
・0:35:47 「設計」と「微分方程式」
設計とは「未来予測」である．その唯一のよりどころは「微分方程式」である．物体の運動や電気・磁気現象を表す微分方程式を「物理法則」という．エンジニアはこれに頼るしかない．
・0:57:20 電気・電子工学の分野の「理論の地図」
SDRにはすべての技術が含まれている．理論の地図を紹介．土台は「初等関数，微分・積分，線形代数」．「通信技術」を学べば「ロボット」も「コンピュータ」も「データ処理」もわかる！全て「線形システムの設計」に見える．
・1:35:28 三角関数
三角関数なしにエンジニアリングは語れない （線形システムの固有ベクトルだから）．「単位円の図」や「加法定理の証明」は一緒に手を動かしてほしい．加法定理の出題例(1999年 東京大学 前期 数学 問1)．
・2:17:25 指数関数 と 対数関数
一見ややこしく見える「対数」の性質は，すべて簡単な「指数法則」から導き出せる！対数は後出の「$e$ の定義や変形」の解説で使うので，自由に使いこなせるようにしておきたい．

●20220226_初めてのソフトウェア無線セミナ【基礎編】_Part2.mp4(3時間39分38秒)

・0:00:00 微分の定義
「局所的な傾き」を表す道具として「微分」を導入する．「1次関数の微分」と「2次関数の微分」はぜひ一緒にやってほしい．$x+\Delta x$を代入した結果から $x$を代入した結果を引き算して，$\Delta x$ で割る．
・0:13:38 三角関数の微分
三角関数の微分ができないと積分ができない．三角関数の積分は【応用編】のフーリエ解析で解説する．「三角関数の微分」には「加法定理」が必要．「暗記」ではなく「自分で理解して導出できる状態」にする．
・0:26:58 微分の性質
微分は「線形」．つまり「まとめて微分したもの」と「個別に微分して足したもの」が一致する．混ざらない．
・0:48:26 指数関数・対数関数の微分
$e$ を「$x=0$における微分係数が 1になる指数関数の底」と決めることで，$e^x$の導関数が$e^x$になる！つまり $e^x$ が相手ならば「微分の記号が消える」ことになる．これで微分方程式も怖くない！
・1:08:07 テイラー展開
どうして 2! とか 3! が出てくるのか直感的に理解する．「無理やり多項式近似」したときの係数$a_0$，$a_1$，…を求めれば「多項式近似できた」ことになる．
・1:51:30 オイラーの公式
$e^{jx}$が複素平面上の単位円上の点になるのは「三角関数の定義そのもの」である．「複素数の極座標表示」は「振幅と位相を簡潔に表す道具」であり，フーリエ解析と非常に相性が良い！
・2:32:41 積分の定義と性質
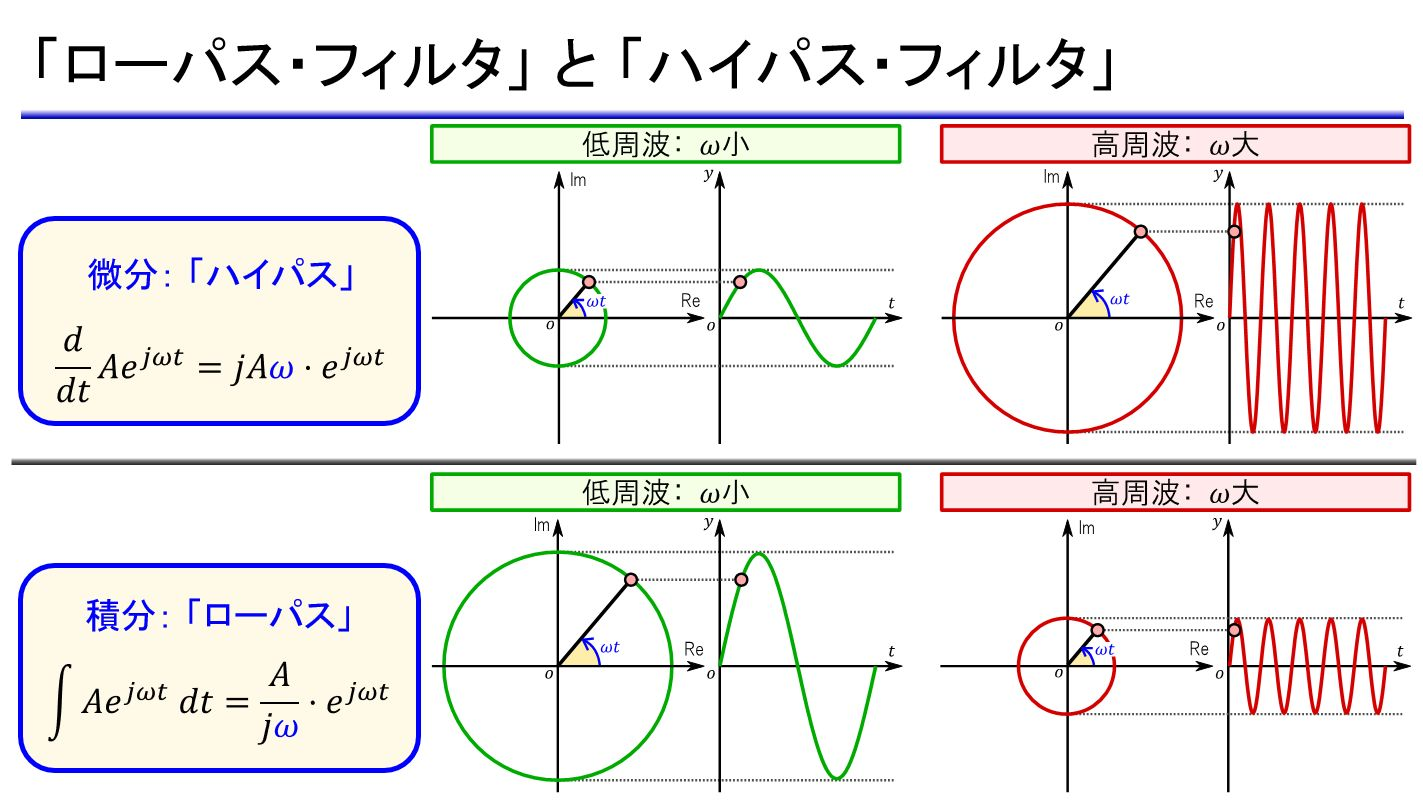
最終的には「微分方程式を解きたい」．グラフで囲まれた面積を求めたい → 長方形で近似する → 人間には無理．「微積分学の基本定理」で微分と積分がつながる！ 積分から「ローパス・フィルタ」の解説へ．「フィルタの原理は微分・積分」.

●20220227_初めてのソフトウェア無線セミナ【応用編】_Part1.mp4(2時間30分59秒)

・0:00:00 イントロダクション
応用編では「微分方程式を解く」．目標は「線形システム」の挙動を「フーリエ解析」という道具によって理解すること．離散時間システムの話のゴールとして「ディジタル・フィルタ」を説明．
・0:13:53 「正弦波」が特別扱いされる理由
電子回路の主役は「乗算回路」と「フィルタ」だった．正弦波に対するこれらの挙動の復習から始める．「線形システムは正弦波と相性が良く，正弦波を使えば微分方程式から微分が消える」→$LCR$回路の例．「様々な波形は正弦波の重ね合わせ作れる」→矩形波の例．
・0:50:55 関数の内積と三角関数の直交性
フーリエ解析で「内積」は超重要．「辺の長さ」ではなく「成分計算」で表すことで「関数の内積」につなげる．関数は「無限次元のベクトル」でその「内積」は「共通成分の大きさ」を表す．
・1:29:02 実フーリエ級数（周期2π）
あらゆる3次元ベクトルを表す素である「基底」の考え方を導入する．cos や sin は「関数の基底」になっているというイメージ．「フーリエ級数」は様々な周波数成分を「ブレンド」している．「フーリエ係数」の抽出は「関数の内積」そのもの．「収束定理」は参考文献を参照．
・1:54:50 実フーリエ級数（周期$2T$）
$\pi /T$という係数を入れることで「周期$2T$」にスケール変更する．規格化の定数が$T$になることを確認する．ここでも「三角関数の加法定理」と「三角関数の微分・積分」を大いに利用する．
・2:04:30 複素フーリエ級数
cosとsinを $e^{j\omega t}$　で置き換えて，都合が良いように「複素フーリエ係数」を定義する．

●20220227_初めてのソフトウェア無線セミナ【応用編】_Part2.mp4(2時間20分10秒)

・0:00:00 フーリエ変換
非周期関数，孤立波形にも対応できるように「周期を∞」にしたものがフーリエ変換．「フーリエ積分公式」の導出が重要．「リーマン和」と見なして積分計算に持ち込むところを丁寧に説明する．積分変数が $x$ なのか $\omega$ なのかを明確に意識することが重要．
・0:21:10 フーリエ変換の性質
「時間領域シフト」の本質は「位相の遅れ」，「周波数領域シフト」の本質は周波数${\omega }_0$の正弦波との「ミキシング」．$f\left(t\right)$が「実数」ならスペクトルは「左右対称」．畳み込みの本質は「ずらして全部足す」だが詳しい話は後出の「線形システム」で説明．
・1:04:16 ラプラス変換
ラプラス変換は「無理やり 絶対可積分 に加工した関数