自動運転やロボットの高精度自動制御の基礎を学べるVOD教材

【キットの組み立て手順書はこちら】
・Part1:初等関数と微分・積分
・Part2:線形代数
・Part3:力学
・Part4:現代制御理論
・Part5:確率・統計
・Part6:カルマン・フィルタ
・Part7:フーリエ解析

■VODサンプル

・関連製品
[講義376分/222頁]Pythonで学ぶ やりなおし数学塾1【微分・積分】
[講義338分/199頁]Pythonで学ぶ やりなおし数学塾2【フーリエ解析】
[講義790分/資料497頁] Pythonで学ぶ マクスウェル方程式 【電場編】＋【磁場編】
[講義ビデオ付き組立キット]初めてのソフトウェア無線＆信号処理プログラミング 基礎編/応用編

・記事を読む
Pythonではじめる 数値解析入門 [Vol.1 Pythonの開発環境をインストールする]
Pythonではじめる 数値解析入門[Vol.2 グラフ描画ライブラリ“Matplotlib”で2次元のグラフを描く]

■自動運転やロボットの高精度自動制御の基礎を学ぶ

●受講対象

・エンジニアリングで共通して使われる「数学」を学びたい方
・ロボット制御の手法である「現代制御理論」を理解したい方
・一般的な「モデル・ベース開発」の考え方を理解したい方
・真値推定アルゴリズム「カルマン・フィルタ」を理解したい方

■Index

●Part1:初等関数と微分・積分

「関数」，「微分・積分」，「線形代数」という3つの分野は，ロボット設計，ディジタル信号処理，電子回路設計など，あらゆる理工学の基礎になっています．Part1では，まず「初等関数」と「微分・積分」の基礎理論を丁寧に解説します．

講義テキストのサンプルを見る

1.イントロダクション
統計学の面白さ/「統計的推定」を行う信号処理
2.初等関数
多項式関数・有理関数/三角関数/指数関数/対数関数
3.微分・積分/1変数関数の微分
1変数関数の積分/オイラーの公式/2変数関数の微分/2変数関数の積分/ガウス積分

●Part2:線形代数

線形代数の基本や線形システムの利点を解説します．線形代数は，後で解説する「現代制御理論」の基礎となります．

講義テキストのサンプルを見る

1.入力・出力がある「システム」を考える
2.線形システムの利点
3.線形代数/ベクトル/行列/行列式/行列と連立1次方程式/固有値と固有ベクトル/対称行列と2次形式

●Part3:力学

力学を学ぶと，ロボットなどの物体の動き方を理解したり予測したりできるようになります．Part3では，「ニュートンの運動方程式」から，力学モデルを作るときに役立つ「ラグランジュの運動方程式」，倒立振子のモデル作成例まで，体系的にわかりやすく解説します．

講義テキストのサンプルを見る

1.イントロダクション
「力学」のキー・ポイント/「運動」のとらえかた
2.力学
ニュートンの運動方程式/オイラーの回転運動方程式/剛体の運動/回転座標系とコリオリカ
3.解析力学
4.倒立振子のモデル作成例

●Part4:現代制御理論

現代制御理論の特徴は，複数の値を同時に扱えることです．この複数の値を同時にフィードバックすることを「状態フィードバック」といいます．状態フィードバックで使うフィードバック・ゲインを効率良く求める手法を「最適制御」といいます．Part4では，システムの安定化に利用される状態フィードバックや最適制御などの制御理論を解説します．ここで説明する状態方程式は，カルマン・フィルタの理解にもつながります．

講義テキストのサンプルを見る

1.現代制御理論のキー・ポイント
2.状態方程式
3.可制御性と可観測性
4.安定性
5.状態フィードバック
6.オブザーバ
7.最適制御

●Part5:確率・統計

確率・統計は，IoTにおけるセンサ・データの解析，AI，電子回路，土木・建築など多くの分野で広く活用されています．Part5では統計学全般で重要な役割を果たす「正規分布」をわかりやすく解説します．

講義テキストのサンプルを見る

1.確率・統計のキー・ポイント
2.記述統計
3.確率の基礎
4.確率変数と確率分布
5.2次元の確率分布
6.正規分布
7.中心極限定理

●Part6:カルマン・フィルタ

無人機やロボットが目的地に向かって走行したり航行したりするには，自分自身の「位置」や「姿勢」を正確に知ることが重要です．しかし，センサによる測定値には必ず誤差が含まれます．カルマン・フィルタは，センサの測定値から誤差を取り除くための技術です．Part6では，自動運転をはじめとする高精度自動制御やデータ解析の分野におけるキー・テクノロジ「カルマン・フィルタ」の理論を基礎から解説します．

講義テキストのサンプルを見る

1.イントロダクション
カルマン・フィルタのキー・ポイント/カルマン・フィルタの動作
2.時系列データ
3.最大事後確率推定(1変数)
4.カルマン・フィルタの導出(1変数)

●Part7:フーリエ解析

フーリエ解析は，信号処理，電子回路，線形システムなどの工学分野に広く利用されている数学的手法です．Part7では，フーリエ解析の考え方の要点をわかりやすく解説します．

講義テキストのサンプルを見る

1.「電気」に関する微分方程式：マクスウェル方程式
2.インダクタとキャパシタの挙動
3.交流回路理論
4.フーリエ変換
5.フーリエ変換と線形性
6.「微分方程式」を「代数方程式」にする
7.ラプラス変換
8.$z$変換

■プログラミング実習用「確率・統計ロボティクス学習キット」付き

●物理法則にもとづくモデルをマイコンに組み込んで操縦させる

1969年，アメリカ航空宇宙局 NASAは38万kmのかなたにある月に宇宙船「アポロ11号(写真1)」をコンピュータで誘導し，無事に着陸させることに成功しました．

アポロ11号のコンピュータ(写真2)は， わずか70行程度のプログラム を利用して宇宙船の位置や姿勢を正確に算出していました．「数理モデル」と「実測値」を利用して確率統計処理によって雑音(誤差)を最小化し，最も確からしい値を短時間で推定する「カルマン・フィルタ」です．

どんなセンサの値にも，「誤差」や「ゆらぎ」といった不要な成分が含まれています．センサの出力値の統計をとると，おおよそ図1のような「正規分布」が得られます．この正規分布の中心が「本当の値」すなわち「真値」であると考えられます．

たくさんのデータの平均をとれば「正規分布の中心」を求められそうですが，実際のリアルタイム処理では図1のように大量のデータを実測するのは困難です．そこで確率・統計の考え方を利用して「真値」にアプローチしようというのが，カルマン・フィルタのアイディアです．カルマン・フィルタを利用すれば，少ないデータをもとにして短時間で「真値」を推定することができます．

アポロ11号が搭載したアルゴリズムは，いわゆるAI（人工知能）の原型ともいえるものです．最近のAIには様々なアルゴリズムがありますが，その中でも教師データを読み込ませてニューラル・ネットワーク上に一種のモデルを構築するという方法がよく知られています．アポロ11号で用いられたカルマン・フィルタにも「計算モデル」は搭載されていましたが，それは自動的な学習によって生成されたものではなく，科学者が自ら用意した「物理モデル」でした．宇宙船に組み込まれたカルマン・フィルタは，「手作業で作ったモデルにもとづいて確率的にもっとも正しそうな値を探すアルゴリズム」ということになります．

1969年当時のコンピュータは何億円もした大がかりなものでしたが，現在は数百円で遥かに高性能なワンチップ・マイコンが手に入ります．今のワンチップ・マイコンを使えば，カルマン・フィルタの処理を十分高速に処理することができます．このキットはカルマン・フィルタによる処理を体験し，その動作原理を理解するために大いに役立ちます．

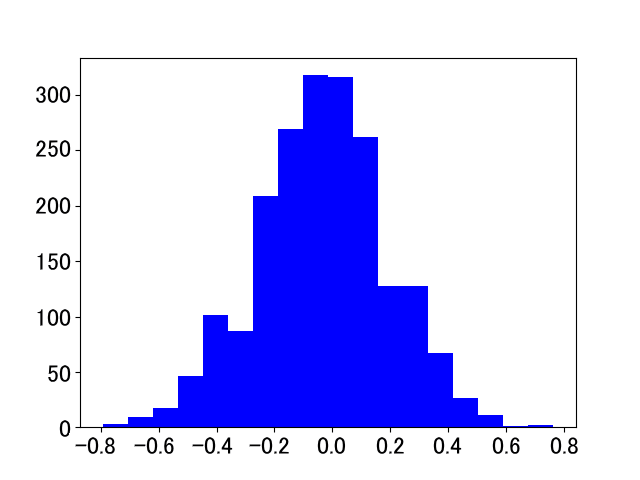写真1: 1969年，NASAは，コンピュータ誘導によって，有人宇宙船「アポロ11号」38万km先にある月まで正確に誘導し着陸させた	写真2: アポロ11号に搭載された誘導用コンピュータ“AGC(Apollo Guidance Computer)”	図1: センサによる測定を何度も繰り返すと正規分布が得られる

●カルマン・フィルタのアルゴリズム

カルマン・フィルタのアルゴリズムは，基本的に4本の数式で表されます．本プログラミング実習キット「確率・統計ロボティクス学習キット」では，この計算をマイコン上で実行してロボットの姿勢推定を行っています．具体的なプログラム例は本ページの末尾に掲載しています．

（1）共分散行列の更新

（2）真値の推定値の計算

（3）1ステップ先の共分散行列の予測